Programming and Quantitative Skills: Extra Practice Questions

Short-Answer Questions (5 points)

Question 1 (1 point)

Calculate \(e^2\) using R:

exp(2)
[1] 7.389056

Question 2 (1 point)

Calculate \(\sqrt[4]{256}\) using R.

256^(1/4)
[1] 4

Question 3 (1 point)

If we create the following vector in R, what class will it be?

c(FALSE, TRUE, "c", "d")
  • Logical.
  • Character.
  • Both logical nd character.
  • Neither logical nor character.

Note: You do not need to supply your code for this question.

x <- c(1, 2, "c", "d")
x
[1] "1" "2" "c" "d"
class(x)
[1] "character"
# All elements of a vector in R must have the same class. Here all elements
# are coerced to be character.

Question 4 (1 point)

Write an R command to generate a numeric vector containing the following sequence:

\[ (0, 2, 0, 4, 0, 6, 0, 8, \dots, 0, 98, 0, 100) \]

1:100 * rep(c(0, 1), times = 50)
  [1]   0   2   0   4   0   6   0   8   0  10   0  12   0  14   0  16   0  18
 [19]   0  20   0  22   0  24   0  26   0  28   0  30   0  32   0  34   0  36
 [37]   0  38   0  40   0  42   0  44   0  46   0  48   0  50   0  52   0  54
 [55]   0  56   0  58   0  60   0  62   0  64   0  66   0  68   0  70   0  72
 [73]   0  74   0  76   0  78   0  80   0  82   0  84   0  86   0  88   0  90
 [91]   0  92   0  94   0  96   0  98   0 100

Question 5 (1 point)

Consider the two vectors below: \[ \begin{split} a &= (1, 4, 8, 2, 5, 6) \\ b &= (2, 4, 6, 8, 10) \end{split} \] Write an R command that returns for each element in \(a\), TRUE if that element is contained anywhere \(b\), and FALSE otherwise. The output should be a logical vector with 6 elements (the number of elements in \(a\)). For example, the first element should be FALSE because 1 is not contained anywhere in \(b\), whereas the second element should be TRUE because 4 is contained somewhere in \(b\).

a <- c(1, 4, 8, 2, 5, 6)
b <- c(2, 4, 6, 8, 10)
a %in% b
[1] FALSE  TRUE  TRUE  TRUE FALSE  TRUE

Data Analysis (5 points)

Download the dataset ceosal.csv. The dataset contains information on chief executive officers (CEOs) at different companies. The variable descriptions are:

  • salary: CEO compensation in 1990 (in dollars).
  • age: CEO age
  • college: \(=1\) if the CEO attended college and \(=0\) otherwise.
  • grad: \(=1\) if the CEO attended post-graduate education and \(=0\) otherwise.
  • comten: Years the CEO worked with the company.
  • ceoten: Years as CEO with the company.
  • profits: Profits of the company in 1990 (in dollars).

Question 6 (1 point)

How many variables are in the dataset?

# First we need to change directory to the folder containing the ceosal.csv
# file. Ideally you would do this using an R project.

df <- read.csv("ceosal.csv")
ncol(df)
[1] 7

Question 7 (1 point)

What is the maximum of the variable comten?

max(df$comten)
[1] 58

Question 8 (1 point)

What is the mean salary of the CEOs aged between 50-59?

mean(df$salary[df$age %in% 50:59])
[1] 796246.9

Question 9 (1 point)

How many CEOs in the dataset didn’t work for their company before becoming the CEO?

# If they joined the company as a CEO, then comten is equal to ceoten:
sum(df$ceoten == df$comten)
[1] 38

Question 10 (1 point)

How old is the best-paid CEO in the dataset?

df$age[df$salary == max(df$salary)]
[1] 64

Data Cleaning (4 points)

Download the dataset euro-dollar-2022.csv. The dataset contains the closing Euro-Dollar exchange rate (variable “Price”) each day throughout 2022, together with the opening, highest and lowest exchange rate. Furthermore, it includes the volume traded and the percentage daily change in the closing price.

In this question you will need clean this dataset to answer the questions that follow.

You should do the following cleaning tasks:

  1. Format the Date variable to a date.
  2. Sort the data by Date ascending (the earliest date in the data should be first, the most recent date last).
  3. Drop rows with any missing data.
  4. Convert Price, Open, High and Low to numeric.
  5. Convert Vol to numeric. For example, "33.87K" should be 33870. Hint: First use the gsub() function to remove the K. Then convert the variable to numeric format. Finally multiply it by 1,000.
  6. Convert Change to numeric. Tip: Use gsub("\\%", "", x) to remove a percentage symbol from x.
  7. Convert all variable names to lower case.

If you did all the steps correctly, you should have 260 observations. The average of the high variable should be 0.9561. The average of the vol variable should be 79,920. If only some of these match your cleaned dataset, you will still be able to answer some of the questions correctly.

# First perform all the cleaning tasks:

df <- read.csv("euro-dollar-2022.csv")

# Format the date:
head(df$Date)
[1] "12/31/22" "12/30/22" "12/29/22" "12/28/22" "12/27/22" "12/26/22"
# Format is MM/DD/YY (year without century):
df$Date <- as.Date(df$Date, format = "%m/%d/%y")

# Order by date:
df <- df[order(df$Date), ]

# Drop observations with missing data:
df <- na.omit(df)

# Convert prices data to numeric:
df$Price <- as.numeric(df$Price)
df$Open <- as.numeric(df$Open)
df$High <- as.numeric(df$High)
df$Low <- as.numeric(df$Low)

# Convert volume to numeric:
df$Vol <- 1000 * as.numeric(gsub("K", "", df$Vol))

# Convert Change numeric:
df$Change <- as.numeric(gsub("\\%", "", df$Change))

# Convert variable names to lower case:
names(df) <- tolower(names(df))

Question 11 (1 point)

Create a variable called open_vs_close which is the open variable minus the price variable. What is the maximum of this variable?

df$open_vs_close <- df$open - df$price
max(df$open_vs_close)
[1] 0.022

Question 12 (1 point)

Use the function wday() from the lubridate package to get the numeric day of the week from the date variable as follows: wday(df$date, week_start = 1). The function returns numbers for each day of the week as follows:

  • 1 means Monday.
  • 2 means Tuesday.
  • 3 means Wednesday.
  • 4 means Thursday.
  • 5 means Friday.

On what day of the week was the lowest volume traded in the dataset?

library(lubridate)
df$weekday <- wday(df$date, week_start = 1)
df$weekday[df$vol == min(df$vol)]
[1] 1

Question 13 (1 point)

What was the largest positive daily price change in the data?

Write the percentage change without the % symbol.

max(df$change)
[1] 1.51

Question 14 (1 point)

What proportion of days did the exchange rate exceed 1.00?

mean(df$price > 1)
[1] 0.1769231

Optimization (3 points)

The following 3 questions will involve working with the following mathematical function defined over all real numbers \(x\):

\[ f(x) = \begin{cases} 3 &\text{ if } x < -1 \\ 8 &\text{ if } x > 4 \\ x^2-2x &\text{ otherwise} \\ \end{cases} \]

Question 15 (1 point)

Plot the function between the \(x\) values \(-3\) and \(+5\). Choose the answer below which best describes the shape of this function:

  • Flat everywhere
  • U shape
  • Inverted U shape (upside-down U)
  • Flat over some ranges of \(x\), and U-shaped in other ranges of \(x\).
  • Flat over some ranges of \(x\), and inverted U-shaped in other ranges of \(x\).

Note: you do not need to save your answer in your R script for this question.

f <- function(x) {
  y <- ifelse(x < -1, 3, ifelse(x > 4, 8, x^2 - 2*x))
  return(y)
}
library(ggplot2)
x <- seq(-3, 5, length.out = 2000)
y <- f(x)
df <- data.frame(x, y)
ggplot(df, aes(x, y)) + geom_line()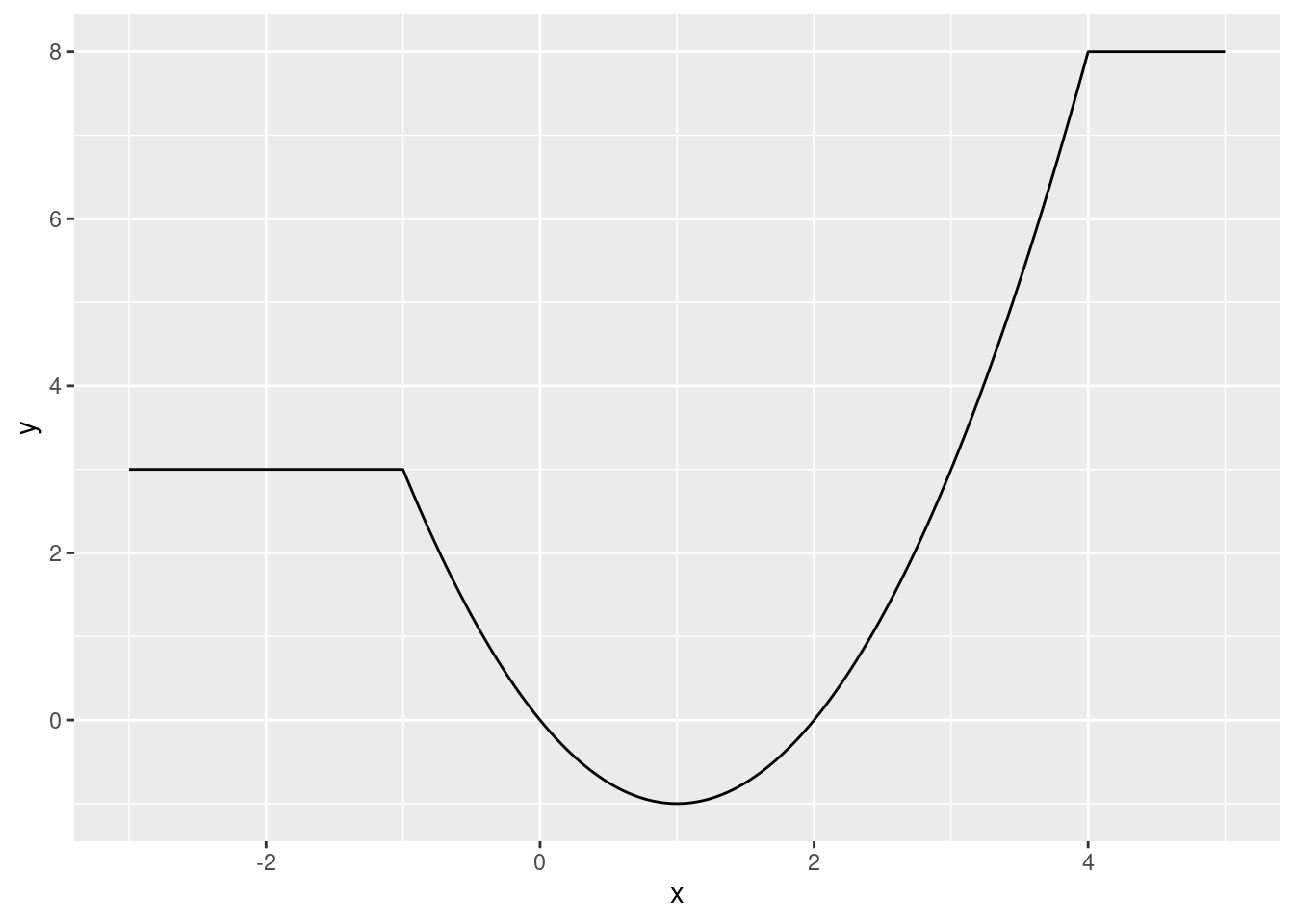

# We can see that it has some flat parts, and a U-shape in other parts.

Question 16 (1 point)

Use R to find the value of \(x\) that minimizes this function. Specify the interval to search over to be \([-1, 4]\).

f_min <- optimize(f, c(-1, 4))
f_min$minimum
[1] 1

Question 17 (1 point)

What value does the function take at the minimum?

f_min$objective
[1] -1
# or alternatively:
f(f_min$minimum)
[1] -1

Aggregating, Merging and Reshaping (3 points)

Download the two datasets:

  1. gdp-per-capita-growths.csv - this dataset contains 3 variables: country, year and gdp_pc_growth. The variable gdp_pc_growth is the growth rate of the country’s per capita gross domestic product (GDP) in that year.
  2. lending-rates.csv - this dataset contains 3 variables: country, year and lending_rate. The variable lending_rate is the lending interest rate in that country in that year.

Question 18 (1 points)

Using the dataset gdp-per-capita-growths.csv, calculate the minimum per capita GDP growth rate each country experienced over the years recorded in the dataset.

Which country had the largest minimum growth rate out of all countries?

df <- read.csv("gdp-per-capita-growths.csv")
tmp <- aggregate(gdp_pc_growth ~ country, data = df, FUN = min)
tmp <- tmp[order(tmp$gdp_pc_growth, decreasing = TRUE), ]
tmp$country[1]
[1] "China"

Question 19 (1 point)

Merge the datasets gdp-per-capita-growths.csv and lending-rates.csv together by the variables "country" and "year", keeping all observations in the gdp-per-capita-growths.csv dataset, but only merging observations from the lending-rates.csv dataset with a match.

Your merged dataset should have 4,087 observations and 4 variables.

How many observations of the variable lending_rate are missing in the merged dataset?

# Read in both datasets:
df1 <- read.csv("gdp-per-capita-growths.csv")
df2 <- read.csv("lending-rates.csv")

# Merge by country and year:
df <- merge(df1, df2, by = c("country", "year"), all.x = TRUE)

# Check that dimensions match the question description:
dim(df)
[1] 4087    4
# Count the number of missing observations in the lending_rate variable:
sum(is.na(df$lending_rate))
[1] 1515

Question 20 (1 point)

Perform the following steps with the lending-rates.csv dataset:

  • Create a subset of the dataset which only includes data on the years 2000 and 2010.
  • Using this subset, reshape the data to wide format with rows representing countries and columns for the country, the lending rate in 2000 and the lending rate in 2010.
  • Drop any rows with missing observations.

Your resulting dataset should have 108 rows and 3 variables. The first three rows should look like:

country      2000     2010
Albania  22.10250 12.82233
Algeria  10.00000  8.00000
 Angola 103.16017 22.54357

What is the mean change in the lending rate from 2000 to 2010 in the dataset? That is, find the mean of the lending rate in 2010 minus the lending rate in 2000.

library(reshape2)

df <- read.csv("lending-rates.csv")
df <- df[df$year %in% c(2000, 2010), ]
df <- dcast(df, country ~ year)
Using lending_rate as value column: use value.var to override.
df <- na.omit(df)
mean(df[, 3] - df[, 2])
[1] -7.554905